 圖、文 •地球人
圖、文 •地球人
圓周360度
羅盤度數
今次的幾何習作跟羅盤有關,為何羅盤跟圓形一周都是360度?
有說來自古代兩河流域的蘇美爾人,其文明距今6500年前。大約4000年前,被巴比倫取代。據說,他們用尺規分圓六分,每分配合其六十進制,於是圓被定為6×60=360度。
又說,本來圓是按太陽在天球上一年一周,而每年大約365.25日,太陽每日行一度。所以,以前分圓為365.25度。之後,為了方便省事,及便於計算,就改為360度。
又方圓二圖?!
今次,小弟嘗試用方圓圖(請參考本欄18年9月「方圓二圖」),以解釋360度的來歷。此圖,其實是正方形加上外接圓。設正方形邊長1單位。外接圓直徑是,正方形邊長乘以2的平方根,1×1.414=1.414單位。所以,外接圓圓周是1.414×π=4.443單位(大約4.44,誤差四千分之一)。正方形周界是4×1=4單位。於是,方圓圖給出兩個重要的比例:
圓周:正方單邊=4.44:1=4.44。
圓周:正方周界=4.44:4=1.11。又是和夫金字塔地基對角線長度一半與其高度之比。
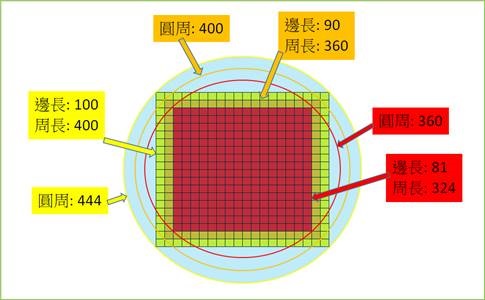
為方便應用,把圖的數值乘以100,就去掉小數。則成為黃色正方單邊=100,正方周界=400,圓周=444。
然後,「方化圓」,用正方形周界400,做一相同圓周的橙色方圓圖。則正方單邊=90,正方周界=360,圓周=400。即是把上一個方圓圖縮小90%。
然後,再「方化圓」,用正方形周界360,做一相同圓周的紅色方圓圖。則正方單邊=81,正方周界=324,圓周=360。即是把上一個方圓圖再縮小90%。
如果,再「方化圓」,用正方形周界324,做一相同圓周的方圓圖。則正方單邊=72.9,正方周界=291.6,圓周=324。正方形單邊出現小數,小數太麻煩,所以不做72.9的方圓圖。而止於紅色方圓圖,就是圓周360。圓周上每單位長度,與圓心形成角度一度。
跟著比例,要弄個正方形邊長63單位,圓周280單位也是可能的。
註:南北朝,大約公元500年。當時,數學家祖冲之已算出圓周率π在3.1415926與3.1415927之間。這是小數後七個位!另外,要多一個數值:2的平方根(2^0.5),1.414。估計當時小數後三個位可以達到了吧。
24×15=360度
精密一些,圓周是81×1.4142×π=359.8701單位。359.8701與360僅相差0.13度或0.0361%。對於這精準度,大概古人會接受吧?!即是說,只要做出一個邊長81單位的方圓二圖,就能用一條刻有360單位長度的繩分圓360度。
如果忠實地這樣分圓,則最後一份只有0.8701度。這個與一度有明顯差別,萬一要求高的皇帝不收貨,怎辦?於是,就不能這樣「忠實」了,要活命,靠取巧。先用圓規分圓為六分,再平分為十二分,再平分為二十四分。在圓周先刻上24條主線。這樣,每兩條主線之間分得360/24=15度。如果主線平分至48條,則兩主線間有7.5度。小數角度不好辦,所以只能分24條主線。這樣,大概也順道解釋了節氣為何,不多不少有24個。(一說是八卦乘三爻共二十四爻。)
分度時,把繩子的起點對正一條主線並緊貼圓弧,在圓弧刻上連續15度。再把繩子的起點對正下一條主線,重覆步驟24次,就可以刻完360度。這樣,就能夠把0.13度誤差平均分攤於24分之中。理論上,每分最後一度之誤差為0.13/24 ,少於0.0055度或0.55%。也許,刻線寬所佔的角度也不只這個數。
另外,還有一招,是首先用尺規把圓平分5份,再平分兩分三次,成為40分。每分9度。每分最後一度之誤差為0.13/40,少於0.0033度或0.33%。誤差更少。如何把圓平分5份嘛,敬請看官參考其他網站或書籍。
**註:以上簡述不代表實際的羅盤製作,只是從理論探討分圓360度的可行性。現代科技發達,羅盤製作肯定比古代更精準可靠。
(本篇完)